factor_analyzerを使って、例題の問題を計算してみたいと思います。本当に使い方があってるのかどうかなどを検証する際には、基本的に誰か偉い人(大学の研究室が出した課題とか)をみながら、こちらもやってみるのがいいと思いますので、中部大学の研究室の問題をベースにやってみたいと思います。なんとか法とかの違いで微妙に数値が違ったりしますが、結果はだいたい同じになるので、あってるということで。
小学生の行動を観察したデータをベースに因子分析を実施する
今回使ったのは、中部大学の心理データを扱っている研究室のデータです。そういえば、私のインテリの同僚社員の方も心理学系で、因子分析をやったと言ってましたので、心理学系のワードと共に例題を探すとよさそうです。
※リンクしてましたが、リンク先が死んでました…
さて、ひとまず、以下で実施
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#日本語が出ないのでフォント読み込んでます
plt.rcParams['font.family'] = 'IPAexMincho'
import seaborn as sns
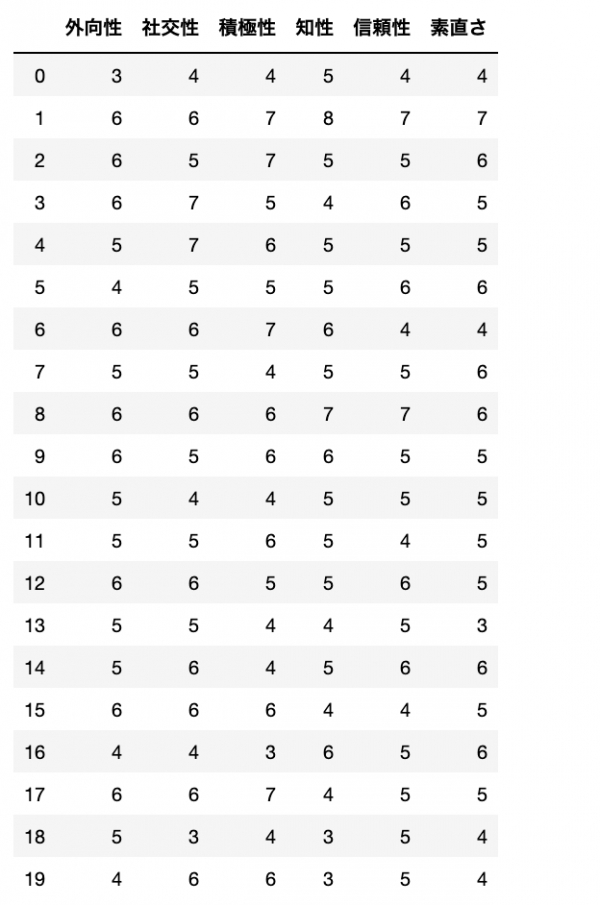
data=pd.read_csv("./syougakusei.csv")
%matplotlib inline
#分析する際に、一番左の番号ってのがいらないので、除去した分析データのみのデータを作る
data_s=data.iloc[:,1:7]
#一旦表示してみる
data_s
こんなデータです。
一旦、各属性がどういう風に影響があるのかみてみます
fig=plt.figure(figsize=(10, 10))
sns.heatmap(data=data_s.corr(),
square=True, vmax=1, vmin=-1, center=0, annot=True, cmap='RdBu_r')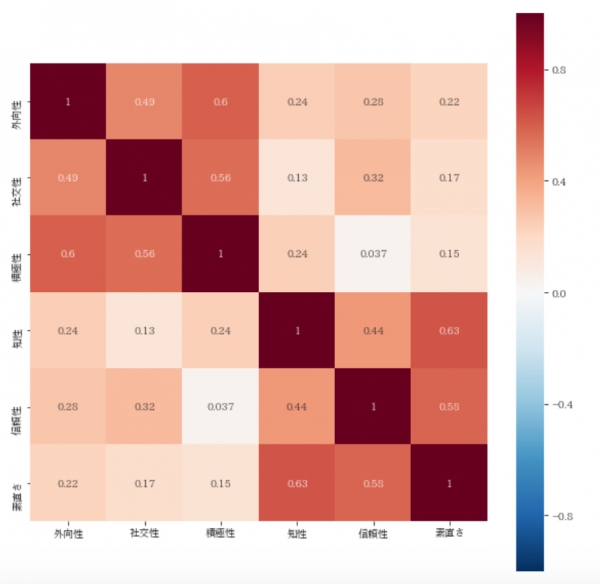
※確率変数とは、ここでいう外交的とかそのあたりのこと。外向性が発生する確率に対する名前。
※相関係数とは、例えば外交的と積極性の間にある関係の強弱のこと。
※正の時は正方向の関係があり、負の時は負方向の相関がある。0の時は相関なし
※corrには引数をあてていないので、デフォルトのピアソンの積率相関係数が使用されてる
ふむふむ。。。
因子的には、
外向性、積極性、社交性
素直さ、信頼性、知性
の2つが仲間っぽいですね
こんなに露骨に色分けされると一発でわかりますね。
でも因子数って2つでいいのかな?
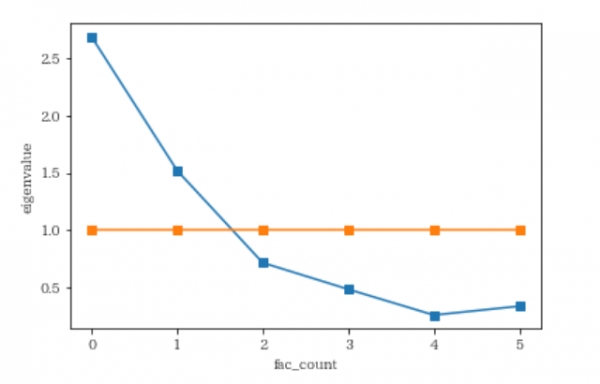
スクリープロットを書いてみます
eigenvalue_one:np.ndarray=np.array([1.0,1.0,1.0,1.0,1.0,1.0])
plt.plot(np.linalg.eigvals(data_s.corr()),"s-")
plt.plot(eigenvalue_one,"s-")
plt.xlabel('fac_count')
plt.ylabel('eigenvalue')
※np.linalg.eigvalsは、行列の固有値を調べる関数
※固有値とは、Ax(ベクトル) =λx(ベクトル) を満たすλのこと。
※スクリープロットとは、固有値を降順でプロットしたグラフのことで、
このグラフをもとに成分数や因子数を決定する方法があるらしい
つまり、この横軸の1より上あたりの因子数がいいらしく、かつ、がっつりグラフがよく下がってるところがいいらしい。
でも今回は2でいきます。大学の研究室の問題が2とご指名です。
from factor_analyzer import FactorAnalyzer
fa=FactorAnalyzer(n_factors=2,rotation="promax",impute="drop")
fa.fit(data_s)
#あとで、因子負荷量の結果にくっつけるために、カラムだしとく
columns=data_s.columns
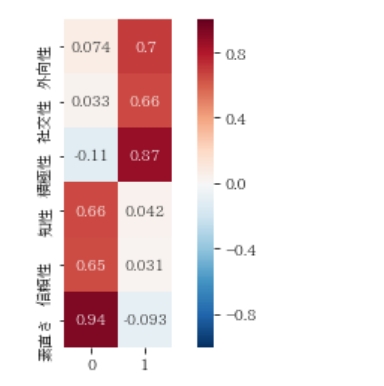
sns.heatmap(data=fa.loadings_,
square=True, vmax=1, vmin=-1, center=0, annot=True, cmap='RdBu_r',yticklabels=columns)ふむ、きっちり分かれましたね。0番の因子は、クラスの真面目系な感じですね。1番の因子は、クラスの明るい感じのアクティブな人っぽいですね。
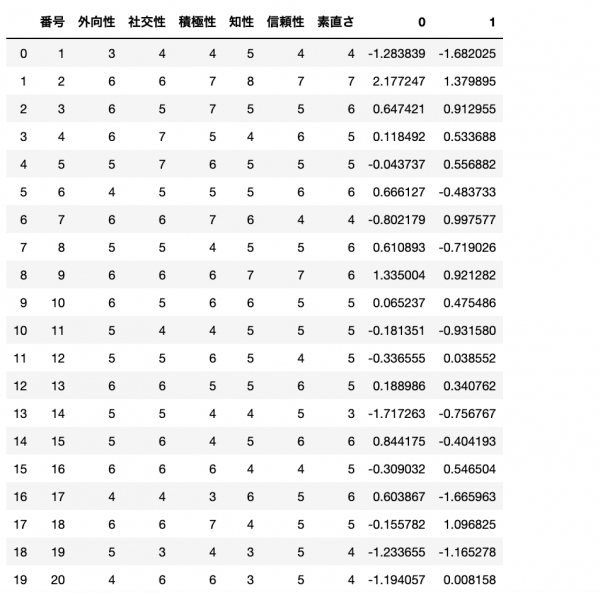
次に、各因子が各クラスメンバーへ与える因子スコアを出してみます
result_data=pd.concat([data,pd.DataFrame(fa.transform(data_s))],axis=1)
result_dataこの右のやつが因子スコアらしいですよ。だからなんだって話なんですけど。